Finding correspondences between Petri net constructs and type system features

15 February 2025 • 18-minute read

This is an exploration of correspondences I observed in my first introduction to a formal tool called Petri nets (PNs) in a class I'm taking this semester and my (yet shallow) existing knowledge on type systems. There will be a primer on both topics for the uninitiated. The ultimate goal is to see if PNs can be encoded to programming language terms where the type checker can determine if the resulting source code is sound, and by extension, the PN, too, seeing that they're a formalization that requires soundness. A question arises: why not just use the techniques native to the field of Petri nets for checking their soundness? The answer is because this entry is actually related to a semester-long project in that class where we are allowed the freedom to explore PNs in relation to our own interests, and my interests lie in programming languge theory and design (not to discount the entire field of PNs, of course).

A primer on Petri nets

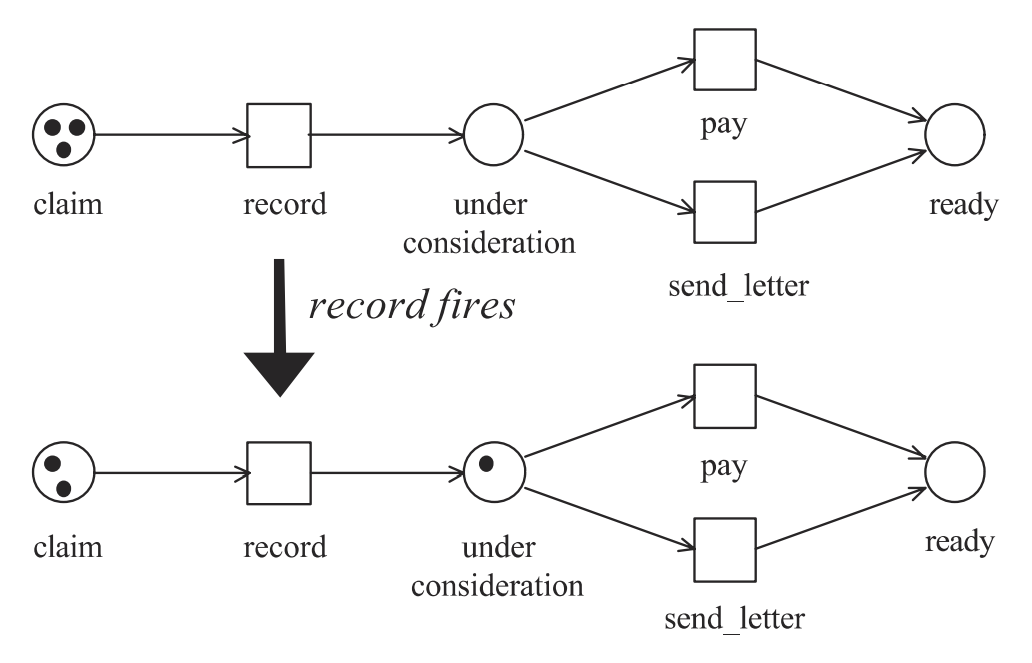
A Petri net is a formal tool for analyzing business processes. A PN is a directed bipartite graph whose nodes are either places (drawn as circles) or transitions (drawn as rectangles). Since it's a bipartite graph, places can only go to transitions and transitions can only go to places. There is a starting place that contains one or more tokens. Tokens trigger the execution of the PN because transitions fire only when all the places that point toward it (called input places) have at least one token each. A transition fires by consuming tokens from its input places and produces tokens to all the places that it points toward to (called output places) and if those places connect to other transitions, they fire next. The execution ends when a token reaches a place that marks the end of the process being modeled. For example, the Petri net below models the process for handling insurance claims.

A primer on type systems

Type systems are systems consisting of rules for how terms in a programming language such as variables, values, function call results are assigned with something a called a type, which restricts what kind of operations can be applied to those terms. Type systems can be informal but we'll be taking a quick look at formal type systems in this entry but I'll refer to them simply as type systems for brevity. Type systems are formalized using natural deduction notation like the following:

This is a type rule that says: "If type String and type Number are valid in some typing environment, an arrow type from String to Number is valid". Arrow types are the types assigned to functions, in this case, say, a function for computing the length of a string: it takes a String parameter and outputs a Number result.

A typing environment can be thought of as an object containing key-value pairs of terms and their types in a scope. It is denoted by \Gamma (gamma). The turnstile ( \vdash ) separates the assumptions in the typing environment from the assertions to the right of it. Altogether, a statement of the form \Gamma \vdash \zeta forms a judgment. In the judgment \empty \vdash true: Boolean , the typing environment can be empty, and this is read as "the term true has type Boolean" (it is assumed that the term true is a built-in constant in the programming language and thus doesn't need a typing environment).

Type rules can have zero or more judgments above the horizontal line (premises) and only one judgment below (the conclusion). A type rule with no premises is an axiom, like the following which says that an empty typing environment is valid:

Analogs between Petri nets and programming languages

A transition in a PN consumes tokens from its input places and produces tokens in its output places. This corresponds to function calls in programming languages with the restriction that the function must have at least one arity and it must have a result. This implies that the Unit type (also known as the Void or Null type) cannot be a valid type if we are to encode PNs to a programming language.

Tokens in a PN inhabit places during execution. Tokens can be thought of as terms in some programming language and places can have associated types mapped to them. Tokens don't 'move' during a PN's execution but are rather consumed and produced. We can then think of a place as a variable that is assigned a value by the result of a function call (in PN terms: after a firing has occurred).

PN transition semantics also imply that once a variable is consumed (in PL terms: supplied as argument in a function call), it can no longer be used for other transitions. Terms can often be reused in programming languages, e.g., a file descriptor being used for reading and writing to a file multiple times, but there are programming languages such as Rust that only allow the usage of a term at most once.

In PNs, assuming it starts with just one token, a place may house a token at most once per process because there might be cases where a transition doesn't produce a token at an output place. This feature of PNs correspond to programming languages like Rust with something called affine type systems that allow usage of terms at most once. (I have not looked deeply into affine type systems as this realization just occurred to me while writing this but I'm sure to get into it as this project progresses).

Sound Petri net constructs

A sound Petri net is called a Workflow net (WN). WNs are PNs with only one start input place and only one end output place. WNs themselves can still have errors, so for guaranteeing soundness, it has to fulfill three requirements. (1) For each token at start, exactly one token must be produced at the end (implies a case eventually completes). (2) If a token is produced at the end, all other places are empty (implies no unfinished tasks). And finally (3), all transitions are able to fire starting from the initial configuration (one token at start) (implies no redundant tasks that never fire).

This entry will talk about the constructive way of checking for soundness of nets. It's possible to produce a sound net from basic building blocks that are themselves sound (but not all sound nets can be conceived this way). The following is taken form the book of Kees Van Hee and Wil van der Aalst titled "Workflow Management: Models, Methods, and Systems".

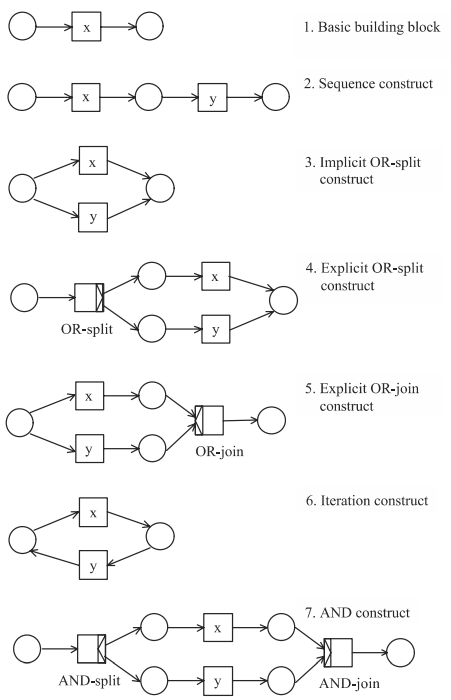
Sound net constructs as programming language features

We now map these sound net constructs to their analog in programming languages. Some of these are more involved than others so they are not presented in order as shown above. This is the part that is largely based upon my observations when my class on Petri nets started. I shall come back and revise this part when my knowledge of type systems get refined.

The basic building block is just a function. We can give it an arrow type A \to B (input place has type A and output place has type B ).

The sequence construct is function composition. If we consider transition x to be a function of type A \to B and transition y to be a function of type B \to C , then their function composition y \circ x has type A \to C . In formal type theory notation:

The iteration construct are just two functions x and y that are inverses of each other.

The AND construct requires one AND-split transition and one AND-join transition. The AND-join transition is the simpler to find correspondence in programming languages: it's just a function with arity equal to the number of incoming arrows or input places. The AND-split transition can be thought of as a function whose output must be compatible to whatever types the functions x and y expect in the example. This is possible using a product type denoted by A \times B , assuming, for example, that function x expects an argument of type A and function y expects an argument of type B . In the actual function call, the value with type A \times B must be deconstructed to two values having types A and B , respectively, then one is chosen whose type matches their respective function's expected parameter type. The product type can be generalized to a tuple type A_1 \times A_2 \times ... \times A_n for cases where an AND-split points towards more than two output places.

The OR-join transition in the explicit OR-join construct can be thought of as a function that can take as argument any one of the types of its input places/functions. This calls for usage of a union type denoted by A | B , assuming for example, that function x produces a value of, say, type A , and that function y produces a value of type B . The union type can be generalized to have more than two types it can possibly have, denoted by A_1 | A_2 | ... | A_n .

The OR-split transition in the explicit OR-split construct represents XOR. In PN semantics, which 'branch' is chosen is largely dependent upon the case being processed. To make this behavior explicit using types, we can set the OR-split function to produce a sum type A | B , where, say, type A could be the input type of function x and type B could be the input type of function y. This way, if the actual value produced is of type A , the transition x fires exclusively, likewise, if the actual value produced is of type B , the transition y fires exclusively.

The fuzziness of the semantics of the implicit OR-split construct is difficult to map in PL terms. The book mentions a time-sensitive example where if a transition fails to do its thing in time, the other transition may fire, making this choice construct simply OR (not XOR). For now, it may be enough to just assign distinct types to the places involved in this construct.

A sketch of an encoding algorithm

Given a workflow net, we do the following:

1. Assign distinct types on every place.

2. Infer the arrow types of the transitions based on input places types and the kind of construct they are based on the observations.

3. Translate the annotated PN into source code of some statically-typed programming language that allows for creation of new types. Places become variables. Transitions become function calls whose parameters are the variables.

The idea is to see if the compiler's type checker complains, then we can conclude that the net is not sound. Due to this encoding scheme being constructive, however, when the type checker doesn't complain, it doesn't imply that the PN is free of flaws. This is similar to how type checkers can guarantee the absence of type errors, but cannot guarantee absence of any other kind of error in programming.

Example 1

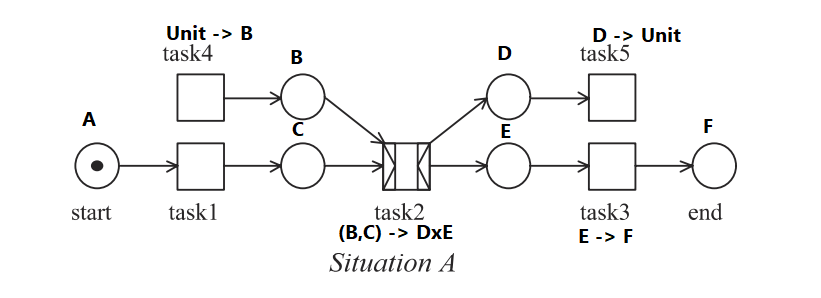
After doing steps 1 and 2, we no longer need to do step 3 because the lack of soundness is evident even just visually: task4 will never fire thus the place having type B will never have a value, thus task2 will never fire because if translated as a function, it has an arity of 2 but it will only get one value, which is from the place having type C after task1 finishes firing.

Example 2

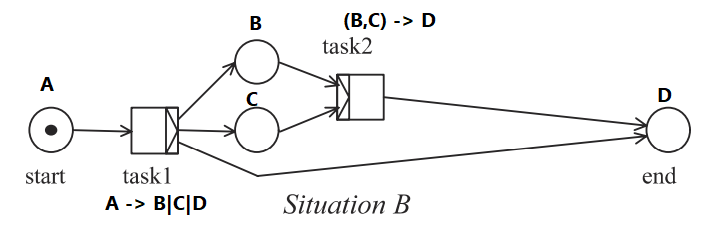
Speaking strictly in terms of programming languages, function task1 produces one value of type B|C|D , while a possible consumer of its result, function task2, requires two paramaters separately of type B and type C . This clearly won't type check; thus the encoded net is not sound.

A programming language I explored to demonstrate the type errors is F# because it is statically-typed and has pattern matching for dealing with sum types. Here is the (failing) code:

        type A = {a: string}

        type B = {b: string}

        type C = {c: string}

        type D = {d: string}

        // We use a random-generator to represent

        // this task sometimes producing B,

        // sometimes producing C, or producing D

        let task1 (a:A) : Choice<B, C, D> =

            let rng = System.Random().Next(1, 100)

            if rng < 75 then Choice1Of3 {b=""}

            else if rng < 50 then Choice2Of3 {c=""}

            else Choice3Of3 {d=""}

        let task2 (b:B, c:C) : D =

            {d=""}

        let start_place: A = {a=""}

        let task1_result: Choice<B, C, D> = task1(start_place)

        let end_place: D = match task1_result with

                | Choice1Of3 b -> task2(b) // Compiler complains there's only type B here, but we have no other value for type C.

                | Choice2Of3 c -> task2(c) // Compiler complains there's only type C here, but we have no other value for type B.

                | Choice3Of3 d -> d

Example 3

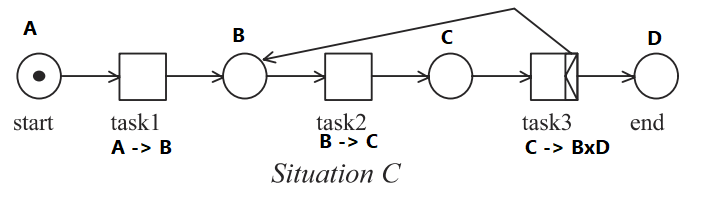
In the book, this net is unsound because while task3 produces a token in the end place, it also produces a token in the place with assigned type B , essentially never terminating. We needed to deconstruct the value produced by task3 to get the value whose type matches that of the end place. With this, the compiler doesn't complain but the scheme fails to recognize the leftover tokens that induces a livelock: trapping a case in an endless cycle. The code can be fiddled with here.

        type A = {a: string}

        type B = {b: string}

        type C = {c: string}

        type D = {d: string}

        let task1 (a:A) : B = {b=""}

        let task2 (b:B) : C = {c=""}

        let task3 (c:C) : B * D = ({b=""}, {d=""})

        let start_place: A = {a=""}

        let b_place: B = task1(start_place)

        let c_place: C = task2(b_place)

        // We deconstructed the value of type BxD

        // by getting the second component indicated by

        // the built-in 'snd' function to get type D

        // which matches the type of d_place

        let d_place: D = snd (task3(c_place))

Example 4

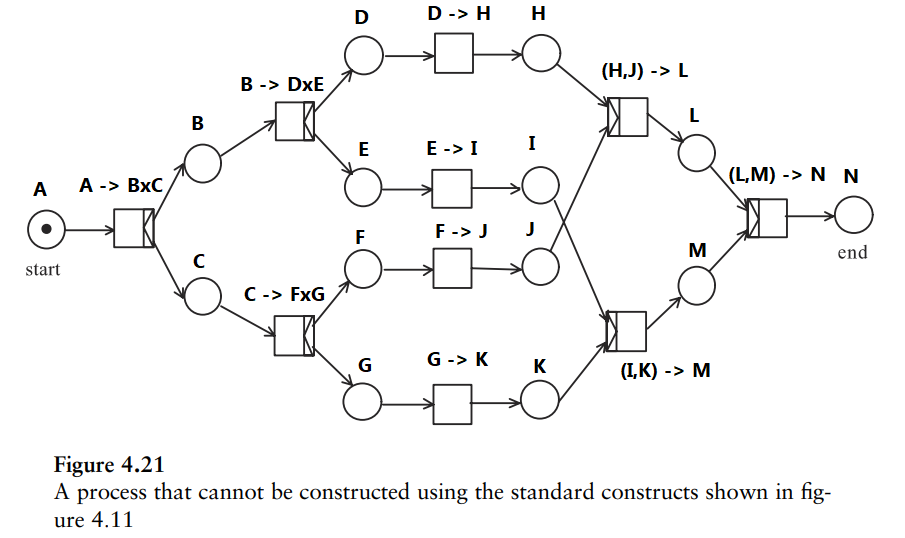
This is a safe net that the book says is not constructible from the basic building blocks of smaller, yet sound constructs. With our scheme however, this can be verified to be sound. Here is the code that doesn't result to type errors:

        type A = {a: string}

        type B = {b: string}

        type C = {c: string}

        type D = {d: string}

        type E = {e: string}

        type F = {f: string}

        type G = {g: string}

        type H = {h: string}

        type I = {i: string}

        type J = {j: string}

        type K = {k: string}

        type L = {l: string}

        type M = {m: string}

        type N = {n: string}

        let a_to_bxc (a:A) : B * C = ({b=""},{c=""})

        let b_to_dxe (b:B) : D * E = ({d=""},{e=""})

        let c_to_fxg (c:C) : F * G = ({f=""},{g=""})

        let d_to_h (d:D) : H = {h=""}

        let e_to_i (e:E) : I = {i=""}

        let f_to_j (f:F) : J = {j=""}

        let g_to_k (g:G) : K = {k=""}

        let h_j_to_l (h:H, j:J) : L = {l=""}

        let i_k_to_m (i:I, k:K) : M = {m=""}

        let l_m_to_n (l:L, m:M) : N = {n=""}

        let start: A = {a=""}

        let b_place: B = fst (a_to_bxc(start))

        let c_place: C = snd (a_to_bxc(start))

        let d_place: D = fst (b_to_dxe(b_place))

        let e_place: E = snd (b_to_dxe(b_place))

        let f_place: F = fst (c_to_fxg(c_place))

        let g_place: G = snd (c_to_fxg(c_place))

        let h_place: H = d_to_h(d_place)

        let i_place: I = e_to_i(e_place)

        let j_place: J = f_to_j(f_place)

        let k_place: K = g_to_k(g_place)

        let l_place: L = h_j_to_l(h_place, j_place)

        let m_place: M = i_k_to_m(i_place, k_place)

        let n_place: N = l_m_to_n(l_place, m_place)

There's this technicality about deconstructing product types in the form of A \times B where we need to get either the first component of type A or the second component of type B to match the type we assigned to a place. We can think of this as some kind of administrative action such that after the AND-split produces two tokens, a resource in the system carries both information at some point in time, and it just knows where to give the one of type A to the appropriate place and the same goes for the one of type B as well.

If we go with this explanation, then the livelock error in Example 3 can be blamed upon this administrative resource in the system not knowing when not to give information, in this case, not to give information of type B back to the B place triggering task2 again. This behavior is not a fault of the Petri net, but a limitation of this scheme. Perhaps if the type system is modified to be linear, where objects can only be used once, this behavior can be resolved, but that's beyond the scope of my knowledge for now. Even with knowledge of linear type systems, if employed in this scheme, my initial hunch is that iteration will break apart since no place can be used more than once.

Conclusion

Petri net constructs can be given analogs in terms of programming language and type system features such as function calls and variables with advanced type constructs such as sum and product types. This can be used in a scheme of encoding a Petri net into source code of some statically-typed programming language and using its type checker to determine if function calls and variable assignments are valid. If they are valid, we mostly conclude that the encoded Petri net is valid (exception we found: livelock detection). If they are not valid, we are sure that the encoded Petri net is not sound. One good thing the scheme does is that it can verify the validity of Petri nets that can't be constructed by the sound basic building blocks.

References:

• Cardelli, Luca. “Type Systems.” ACM Computing Surveys, vol. 28, no. 1, Mar. 1996, pp. 263–64.
• Van Der Aalst, W., & Van Hee, K. M. (2004). Workflow Management: Models, Methods, and Systems. MIT press.